Content
Lossy and lossless image compression.
- Changing colour spaces and subsampling
- DCT and quantisation
- Run-length encoding
- Entropy coding
Audiovisual Processing CMP-6026A
Dr. David Greenwood
December 01 2021
Lossy and lossless image compression.
How can we compress an image without destroying the image?
Inter-pixel redundancy:
Coding redundancy:
Pycho-visual redundancy:
\[ \begin{aligned} Y &= 0.299R + 0.587G + 0.114B \\ C_b &= B-Y \\ C_r &= R-Y \end{aligned} \]
\[Y = 0.299R + 0.587G + 0.114B\]
Humans are more sensitive to luminance…
\[ \begin{aligned} C_b &= B-Y \\ C_r &= R-Y \end{aligned} \]
Humans are less sensitive to chrominance…
We can downsample the chrominance channels without affecting the image in a perceptible way.
Subsampling scheme is expressed as a ratio J:a:b
Transforms the image into the frequency domain.
Reduce the number of bits needed to store a value by reducing precision.
Quantisation is performed as follows:
\[DCT_{q}(i, j) = round \left( \frac{DCT(i, j)}{Q(i, j)} \right)\]
where \(Q\) is the quantisation matrix.
\(65, -27, -2, 17, -3,\) \(19, 0, -3, 8, 0, ...\)
Reads from low frequency coefficients to high frequency coefficients…
More likely to encode all non-zeros and all zeros together…
Extracts series of value and length of runs from sequence of values.
Exploits inter-pixel redundancy.
65 -27 -2 17 -3 -3 1 1 1 -2 1 1 0 -1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
65 -27 -2 17 -3 -3 1 1 1 -2 1 1 0 -1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
65 1 -27 1 -2 1 17 1 -3 2 1 3 -2 1 1 2 0 1 -1 1 1 1 0 19
65 -27 -2 17 -3 -3 1 1 1 -2 1 1 0 -1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
65 1 -27 1 -2 1 17 1 -3 2 1 3 -2 1 1 2 0 1 -1 1 1 1 0 19
65 -27 -2 17 -3 -3 1 1 1 -2 1 1 0 -1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
65 1 -27 1 -2 1 17 1 -3 2 1 3 -2 1 1 2 0 1 -1 1 1 1 0 19
65 -27 -2 17 -3 -3 1 1 1 -2 1 1 0 -1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
65 1 -27 1 -2 1 17 1 -3 2 1 3 -2 1 1 2 0 1 -1 1 1 1 0 19
Exploits inter-pixel redundancy
Information and data are not the same thing.
Entropy Coding exploits coding redundancy
Entropy Coding encodes a sequence with variable length code so that:
The new alphabet requires fewer bits per pixel.
Recall: the probability of an event is:
\[p_{i} = \frac{N_{i}}{N}\]
The information in bits is:
\[I_{i} = - \log_{2} p_{i}\]
The entropy, the smallest possible mean symbol length, is:
\[H = - \sum_{i} p_{i} \log_{2} p_{i}\]
We can use these properties to develop a better coding for an image.
Step 1:
Step 2:
Step 3:
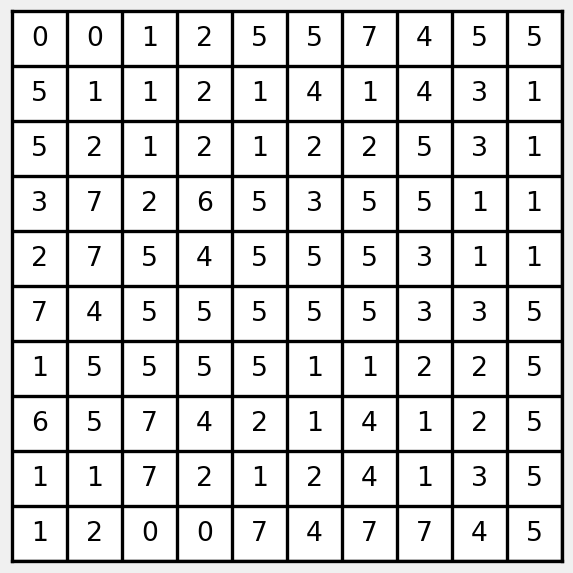
What is the Huffman code for this image?
And, what is the current bit rate?
Count the frequencies of each symbol.
| Frequency | Symbol |
|---|---|
| 4 | 0 |
| 23 | 1 |
| 15 | 2 |
| 8 | 3 |
| 10 | 4 |
| 29 | 5 |
| 2 | 6 |
| 9 | 7 |
What is the entropy of this image?
| \(p(s)\) | \(-\log p(s)\) | \(\times\) |
|---|---|---|
| 0.29 | 1.786 | 0.518 |
| 0.23 | 2.120 | 0.488 |
| 0.15 | 2.737 | 0.411 |
| 0.10 | 3.322 | 0.332 |
| 0.09 | 3.474 | 0.313 |
| 0.08 | 3.644 | 0.292 |
| 0.04 | 4.644 | 0.186 |
| 0.02 | 5.644 | 0.113 |
| \(+\) | 2.651 |
Sort by the most frequent symbol.
| Frequency | Symbol |
|---|---|
| 29 | 5 |
| 23 | 1 |
| 15 | 2 |
| 10 | 4 |
| 9 | 7 |
| 8 | 3 |
| 4 | 0 |
| 2 | 6 |
Merge the two leaves with the lowest frequency…
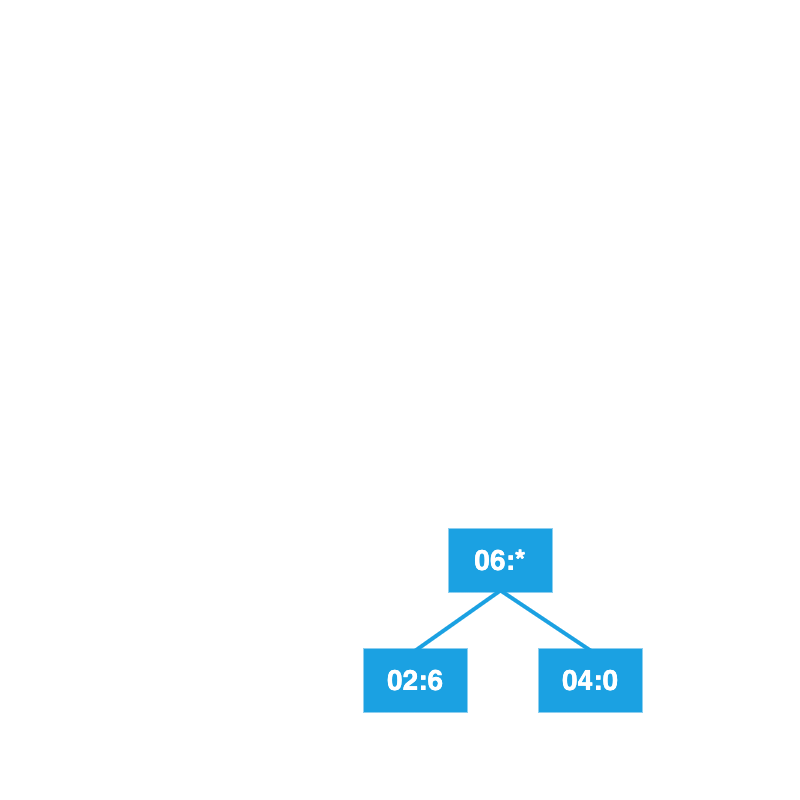
Insert the node into the sorted list.
| Frequency | Symbol |
|---|---|
| 29 | 5 |
| 23 | 1 |
| 15 | 2 |
| 10 | 4 |
| 9 | 7 |
| 8 | 3 |
| 6 | * |
Repeat with the next two lowest frequencies.
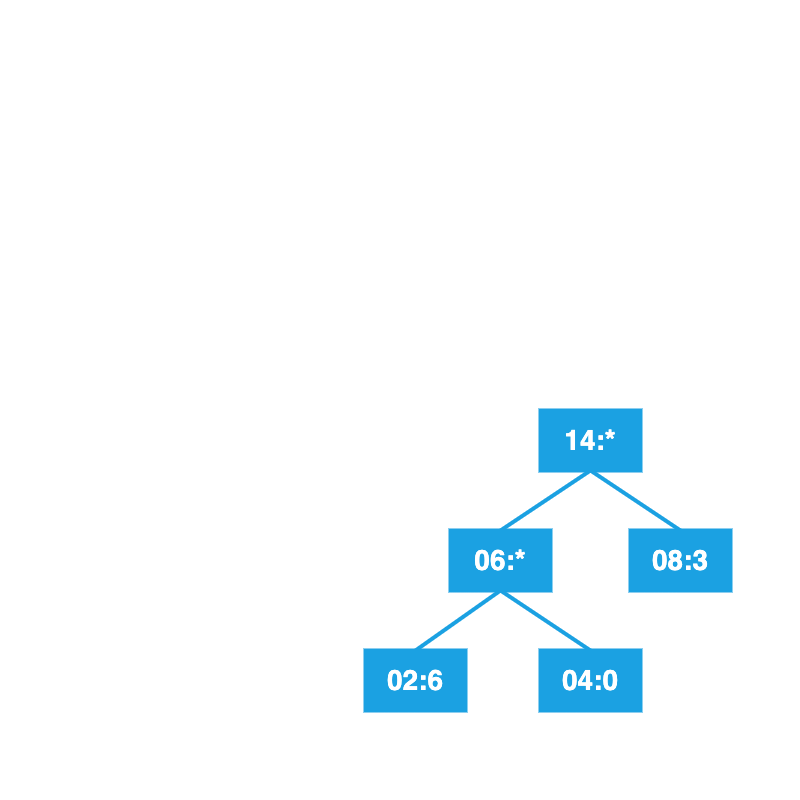
Insert the node into the sorted list.
| Frequency | Symbol |
|---|---|
| 29 | 5 |
| 23 | 1 |
| 15 | 2 |
| 14 | * |
| 10 | 4 |
| 9 | 7 |
Repeat with the next two lowest frequencies.
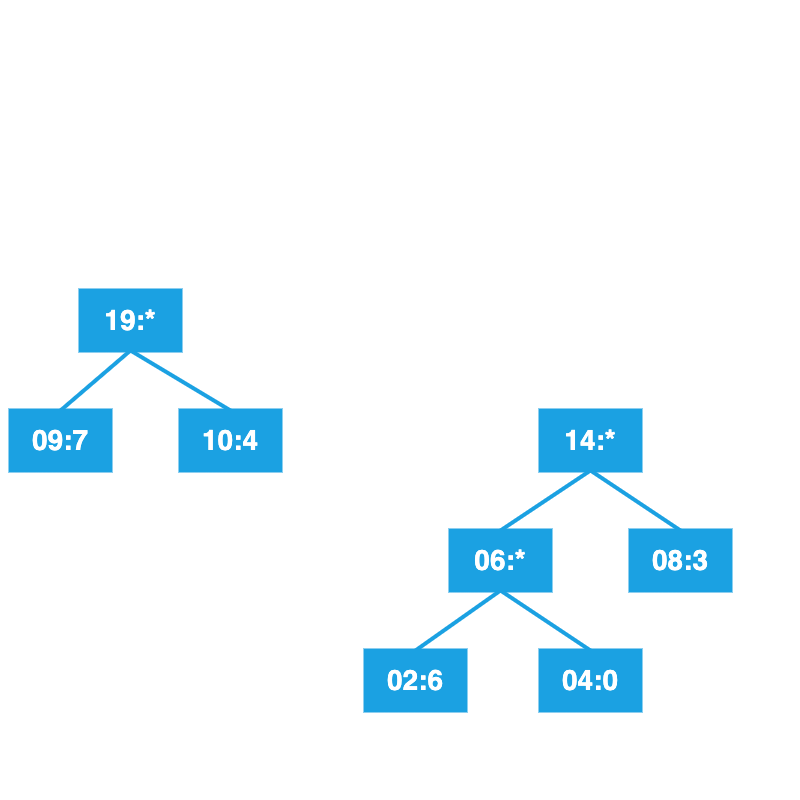
Continue until the tree is complete.
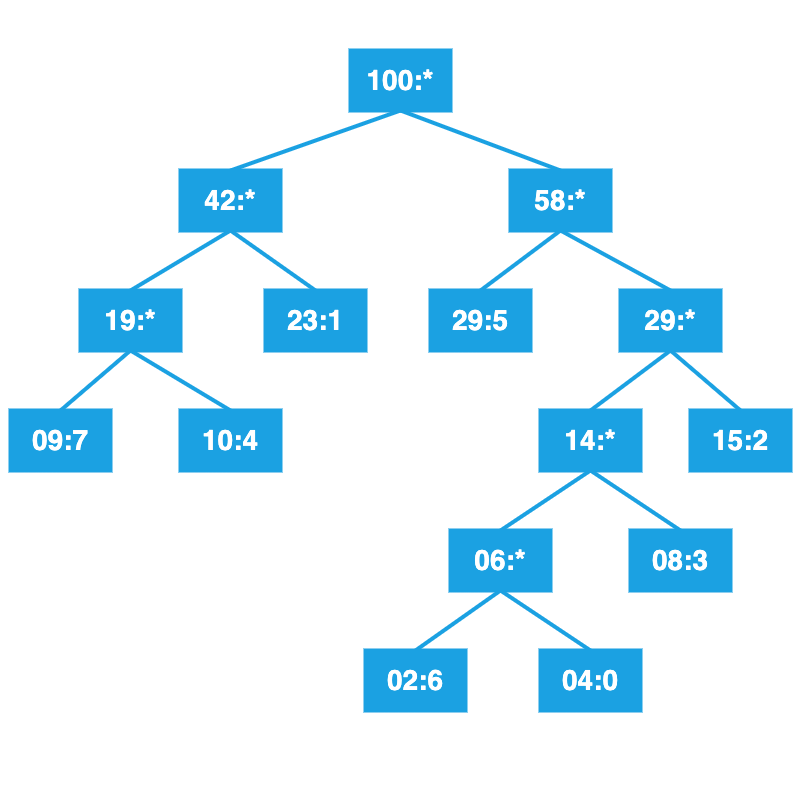
Label left branches with 0, right branches with 1.
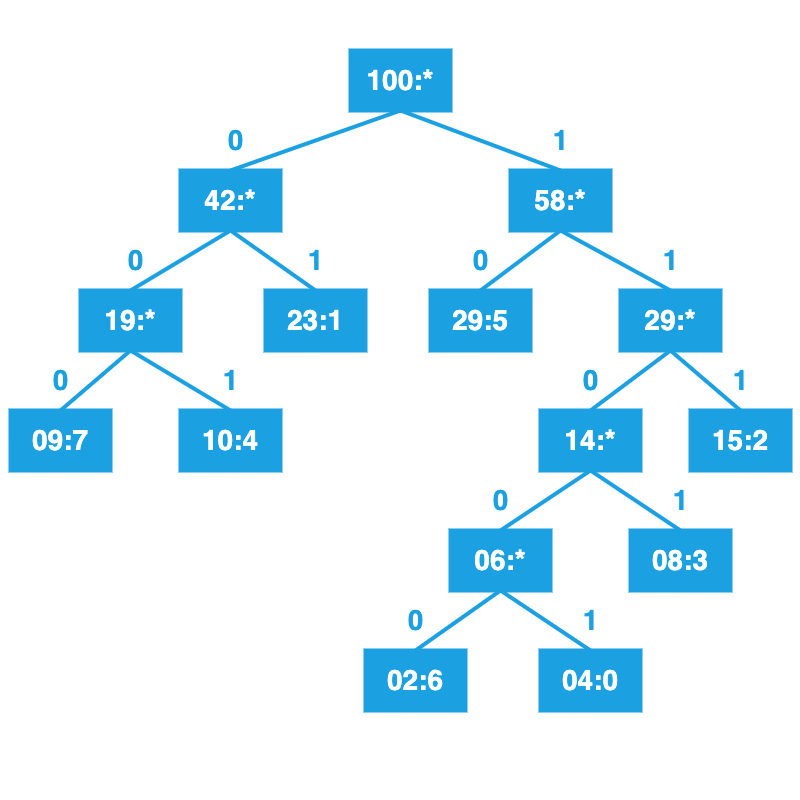
Read from the root to compute the new codes.
| Code | Symbol |
|---|---|
| 11001 | 0 |
| 01 | 1 |
| 111 | 2 |
| 1101 | 3 |
| 001 | 4 |
| 10 | 5 |
| 11000 | 6 |
| 000 | 7 |
| Value | p(x) | code length | \(\times\) |
|---|---|---|---|
| 5 | 0.29 | 2 | 0.58 |
| 1 | 0.23 | 2 | 0.46 |
| 2 | 0.15 | 3 | 0.45 |
| 4 | 0.10 | 3 | 0.30 |
| 7 | 0.09 | 3 | 0.27 |
| 3 | 0.08 | 4 | 0.32 |
| 0 | 0.04 | 5 | 0.20 |
| 6 | 0.02 | 5 | 0.10 |
| + | 2.68 |
We can calculate the bit rate we achieved.
Three types of redundancy are exploited in image compression.