Non-Linear Image Filtering

Audiovisual Processing CMP-6026A

Dr. David Greenwood

Content

  • Order Statistics filters
  • Morphological filtering
  • Morphological operations for object detection
  • Morphological operations for edge detection

Order-Statistics Filters

Linear filters compute the sum of products between kernel coefficients and the image neighbourhood.

Instead, replace intensity with a measure obtained by ordering the pixel intensities in the neighbourhood.

  • Common filters are median, max and min.

Crop a part of a larger image to uses as an example.

Cameraman crop

First, window a region of size 3x3:

region window

Sort the intensities in the region:

ordered values

Sort the intensities in the region, and select the middle value:

median value

Max filter is similar to median filter, but selects the maximum value:

maximum value

Min filter is again similar, but selects the minimum value:

minimum value

Order-statistics filters are good for noise removal where:

  • Noise is random
  • Noise is not dependent on surrounding pixels

For example, the salt and pepper noise model:

  • Noisy pixels are the outliers in the local neighbourhood
  • Replace outliers with estimate from image data

Aside: What is salt and pepper noise?

  • Also called impulse noise.
  • Can be hardware dependent - hot pixels or dead pixels.
  • Artificially applied by random selecting a subset of pixels and setting to black or white.

Median Filter

salt and pepper noise, P=0.1

Median Filter

noisy and median filtered images

Median Filter

original and median filtered images

Median Filter

difference image

Median Filter

gaussian and median filtered images

Noise removal

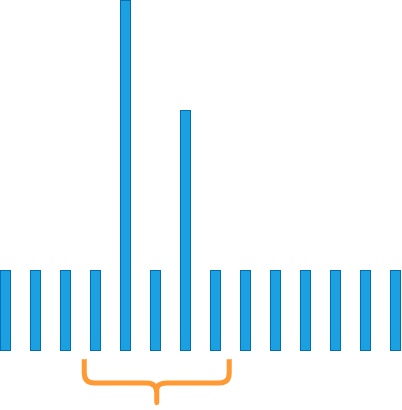
If we consider this 5 pixel neighbourhood, what will the median filter do?

Noise removal

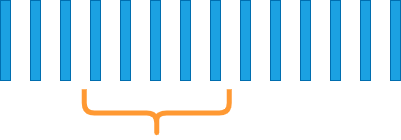
The median filter removes spike noise.

  • What will the gaussian filter do?

Noise removal

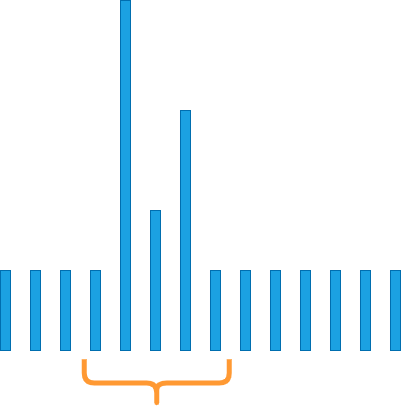
The Gaussian filter amplifies noise.

Morphological Filters

Morphological Filters

Operation of the filter is characterised by mathematical morphology.

  • Embedded in set theory.
  • Useful for thickening and thinning edges and de-noising binary images

Motivation

Filtered Threshold Image

Morphological Filters

For binary images:

  • White pixels (with intensity 1) can be considered elements in a set.
  • Black pixels (with intensity 0) can be considered elements outside of the set.
  • Morphological filters are essentially set operations.

Set Notation

\[\text{Let } A \text{ be a set in } \mathbb{Z}^{2}\]

the set of all integers in 2 dimensions…

Set Notation

\[ a \in A \text{ if } a = (x, y) \text{ is an element of set } A \]

this is the element symbol…

Set Notation

\[ a \notin A \text{ if } a \text{ is not in } A \]

not in…

Set Notation

\[ C = \{ w|w = -d, ~ for ~ d \in D \} \]

the set of all \(w\) such that…

Set Notation

\[\emptyset \text{ is the empty set} \]

Set Operations

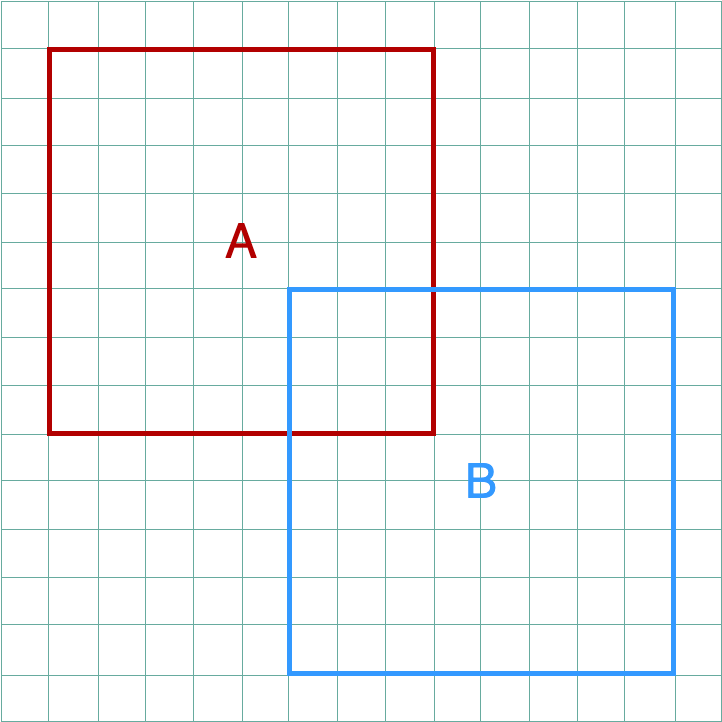
Given two sets, A and B, the following can be defined:

Set Operations

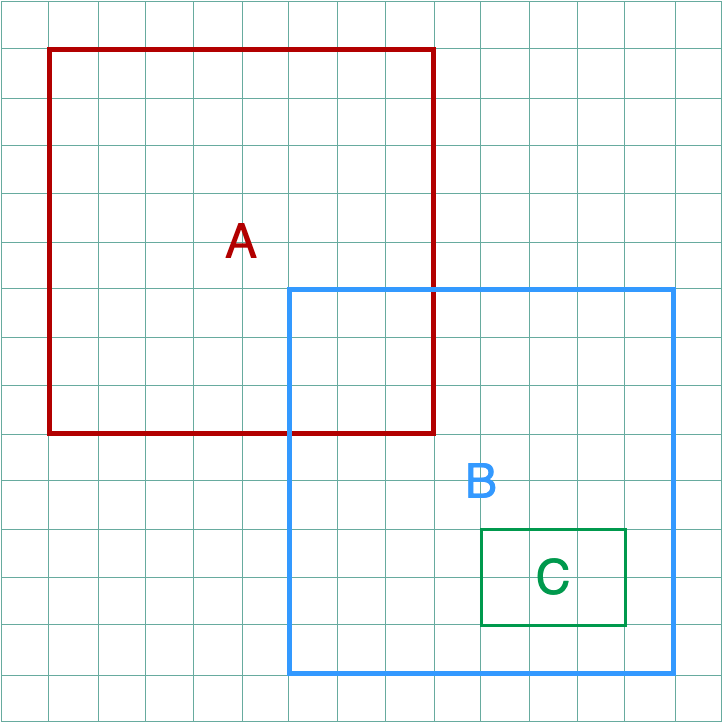
\[C \subseteq B, A \nsubseteq B\]

Subset: a set where all members belong to a given set.

Set Operations

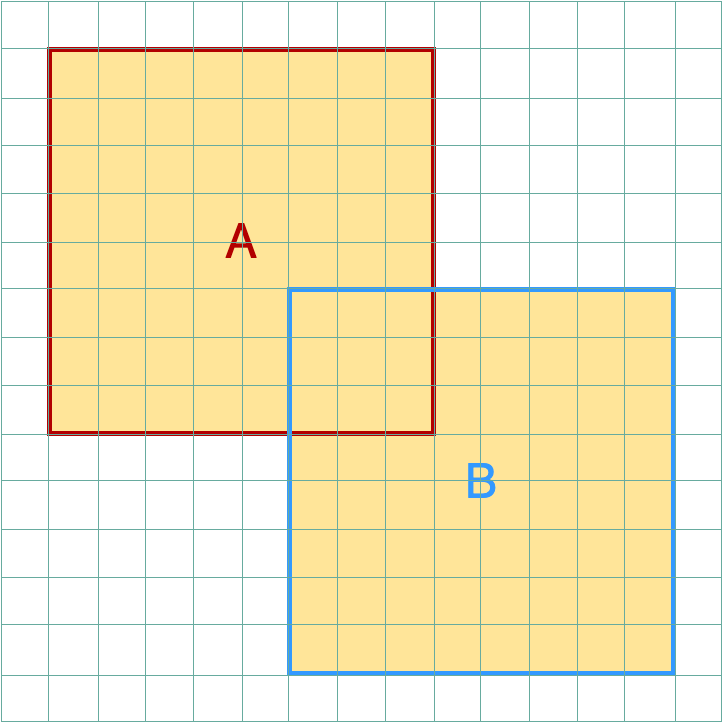
\[A \cup B\]

Union: all elements that are either in set A or set B.

Set Operations

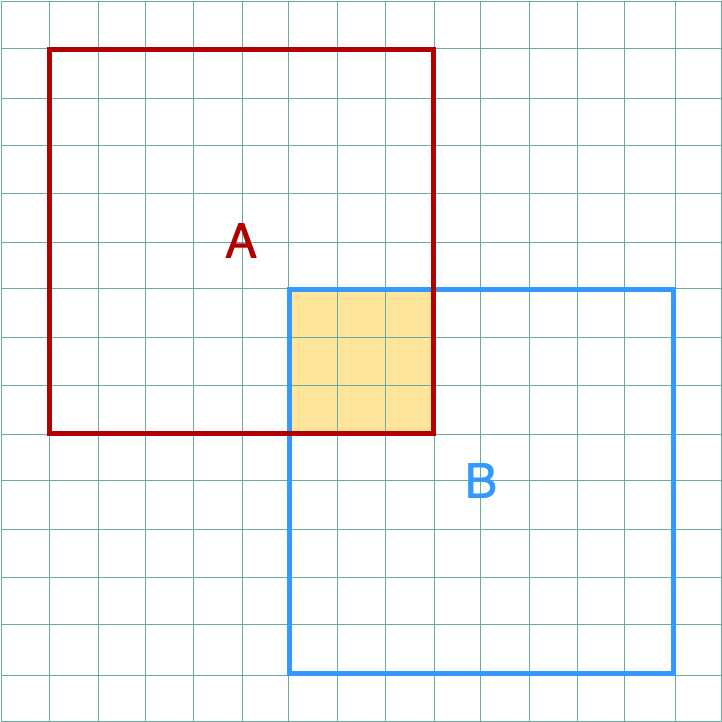
\[A \cap B\]

Intersection: all elements that are common to both A and B.

Set Operations

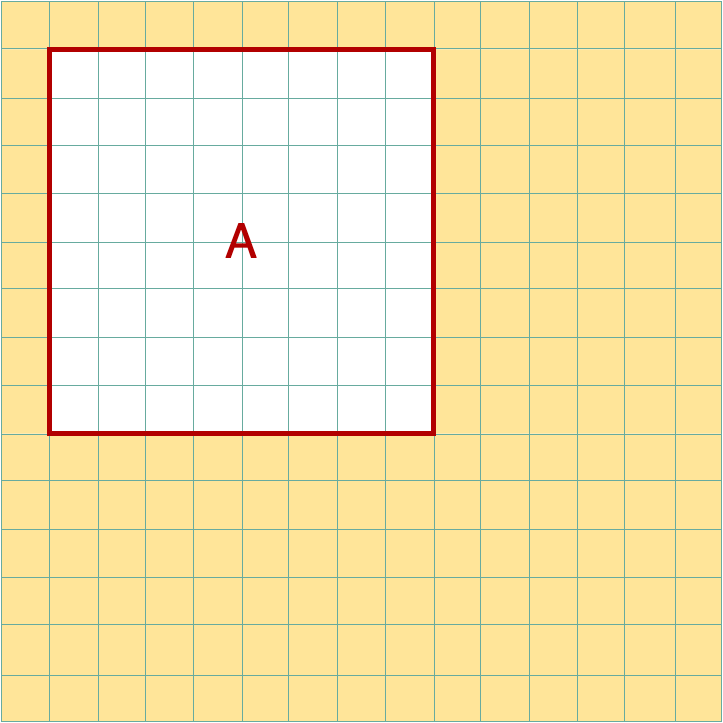
\[A^{c} \{w|w ~\notin ~ A\}\]

Complement: the elements not contained in set A

Set Operations

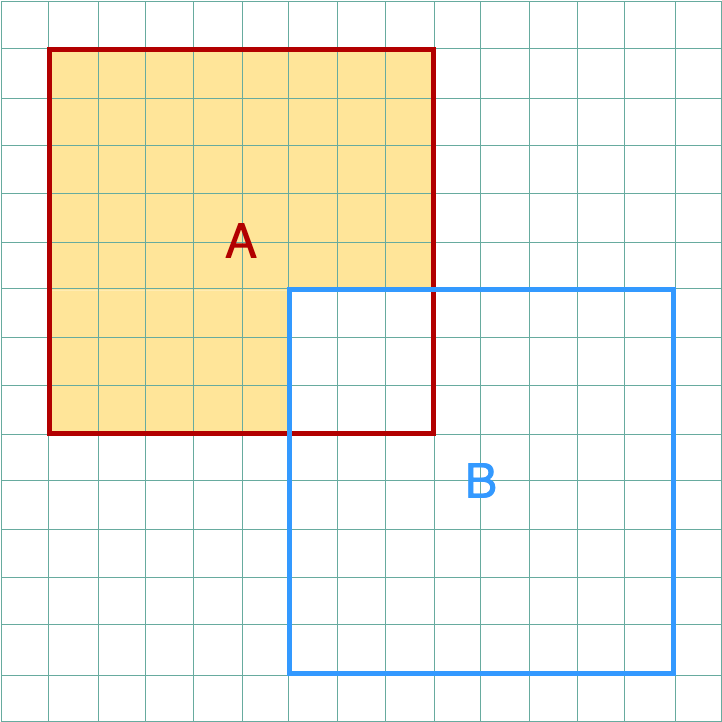
\[A \setminus B = \{w|w ~\in ~ A,~ w ~\notin ~ B \}\]

Difference: the elements of set A that are not in set B

Structuring Element

A binary image (or mask) that allows us to define neighbourhood structures.

Structuring Element

  • Can be different sizes: larger structuring elements produce a more extreme effect.
  • Can be different shapes: common to use a disk or cross shape.
  • Has a defined origin: usually at the centre.

Structuring Element

Structuring Element

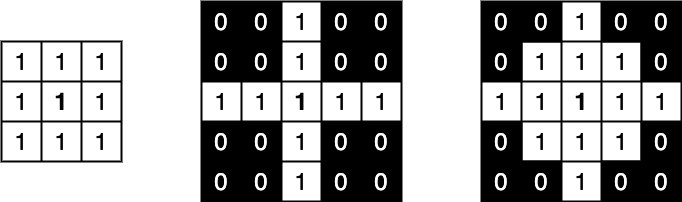
A structuring element is said to fit the image if, for each of its pixels set to 1, the corresponding image pixel is also 1.

The set of all displacements such that the image and the structuring element overlap at every pixel.

Structuring Element

A structuring element is said to hit, an image if, at least for one of its pixels set to 1 the corresponding image pixel is also 1.

The set of all displacements such that the image and the structuring element overlap at any pixel.

Morphological Operators

Dilation

\[A \oplus B = \{ x, y| B_{x, y} \cap A \neq \emptyset \} \]

Defines dilation of binary image \(A\) by structuring element \(B\).

Calculate the binary OR of elements in \(A\) masked by \(B\).

The structuring element hits the image.

Dilation

binary image

\[A \oplus B\]

structured element

Dilation

binary image
dilated image

Dilation Example

dilation 5x5

Dilation Example

dilation 15x15

Dilation

  • Expands the size of 1-pixel objects
  • Smoothes object boundaries
  • Closes holes and gaps
  • Regions grow

Erosion

\[A \ominus B = \{ x, y| B_{x, y} \subseteq A \} \]

Defines erosion of binary image \(A\) by structuring element \(B\).

Calculate the binary AND of elements in \(A\) masked by \(B\).

The structuring element fits the image.

Erosion

binary image

\[A \ominus B\]

structured element

Erosion

binary image
eroded image

Erosion Example

erosion 5x5

Erosion Example

erosion 15x15

Erosion

  • Shrinks the size of 1-valued objects.
  • Smooths object boundaries.
  • Removes peninsulas, fingers, and small objects (such as noise).

Opening

\[A \circ B = (A \ominus B) \oplus B \]

Erosion followed by Dilation.

  • Has the effect of smoothing contours by breaking narrow connections and eliminating thin protrusions.

Opening Example

opening 5x5

Opening Example

opening 15x15

Closing

\[A \bullet B = (A \oplus B) \ominus B \]

Dilation followed by Erosion.

  • Has the effect of smoothing contours by filling narrow gulfs, holes and small gaps.

Closing Example

closing 5x5

Closing Example

closing 15x15

QUESTION?

After performing dilation of A by B, what does the resulting binary image look like?

Answer

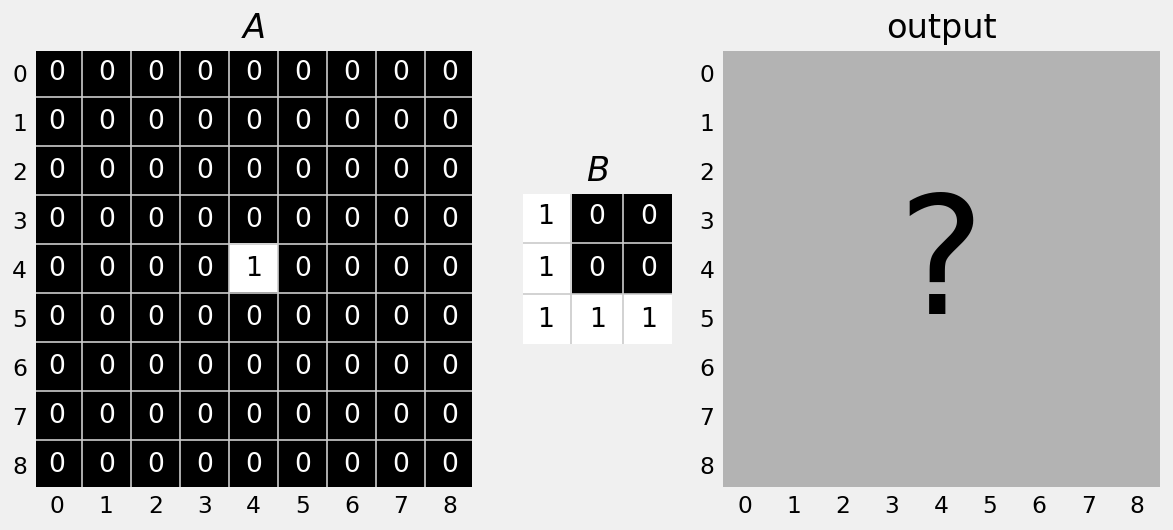
After performing dilation of A by B, what does the resulting binary image look like?

Morphological Operations for Object Detection

Object Detection

Original image A

Object Detection

A
B

\(A \circ B\)

Morphological Operations for Edge Detection

Edge Detection

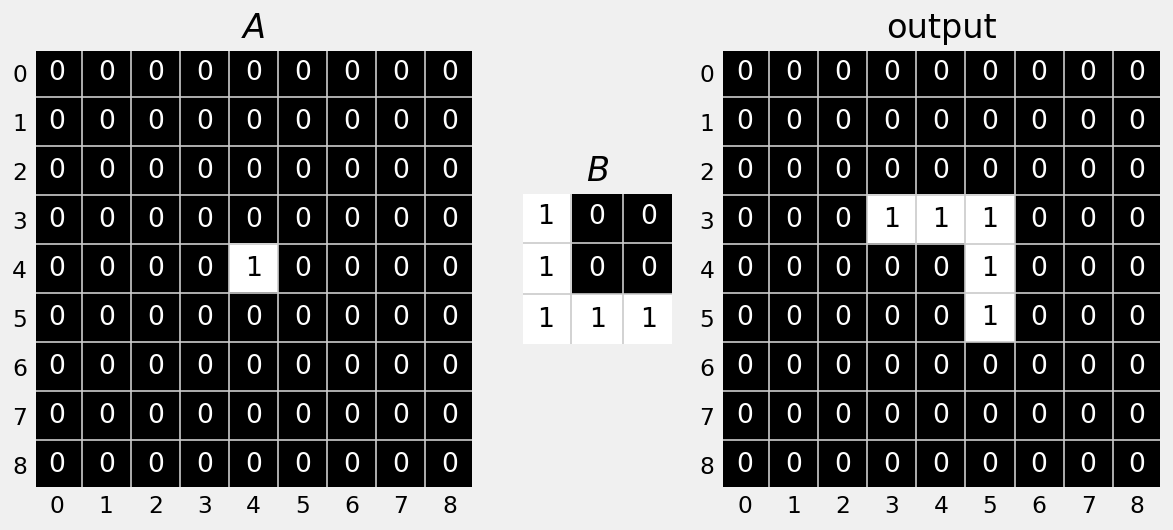
Using difference images, we can detect edges.

  • Dilation of A by structural element B, followed by difference with A.
  • Erosion of A by B, followed by difference with A.
  • Dilation of A by B, followed by difference with erosion of A by B.

Edge Detection

binary A

Edge Detection

\[(A \oplus B) - A\]

Dilation Difference image.

Edge Detection

\[(A \ominus B) - A\]

Erosion Difference image.

Edge Detection

\[(A \oplus B) - (A \ominus B)\]

Dilation Erosion Difference.

Further Reading

Digital Image Processing

  • Rafael C. Gonzalez
  • Richard E. Woods

Summary

  • Order Statistics filters
  • Morphological filtering
  • Morphological operations for object detection
  • Morphological operations for edge detection
// reveal.js plugins