How do we describe keypoints in a way that similar points can be matched?

Keypoint and Descriptor

An important distinction:

Keypoint and Descriptor

keypoint: \((x, ~y)\)

descriptor at the keypoint:

\[ \begin{bmatrix} 0.02 \\ 0.01 \\ 0.10 \\ 0.05 \\ 0.01 \\ ... \end{bmatrix} \]

Descriptors

• HOG: Histogram of Oriented Gradients
• SIFT: Scale Invariant Feature Transform
• SURF: Speeded-Up Robust Features
• GLOH: Gradient Location and Orientation Histogram
• BRIEF: Binary Robust Independent Elementary Features
• ORB: Oriented FAST and rotated BRIEF
• BRISK: Binary Robust Invariant Scalable Keypoints
• FREAK: Fast REtinA Keypoint

… and many more

Descriptors

Describing a keypoint.

SIFT Features

Image content is transformed into features that are invariant to:

• image translation
• image rotation
• image scale

SIFT Features

SIFT Features are partially invariant to:

• illumination changes
• affine transformations and 3D projections

SIFT Features

SIFT Features are suitable for detecting visual landmarks:

• from different angles and distances.
• with a different illumination.

DoG over Scale-Space Pyramid

Over different image pyramid levels:

1. Gaussian smoothing.
2. Difference-of-Gaussians (DoG) and find extrema.
3. Maxima suppression for edges.

SIFT Features

A SIFT feature is given by a vector computed at a local extreme point in the scale space.

SIFT Features

SIFT Features

SIFT Features

From an input image we convert to grey scale then compute the Difference of Gaussians (DoG) and find the extrema.

SIFT Features

We preserve the scale, and compute a peak of the histogram of orientations.

SIFT Features

We compute a local patch, based on the scale and orientation.

It is from this patch we compute the 128D feature descriptor vector.

SIFT Descriptor

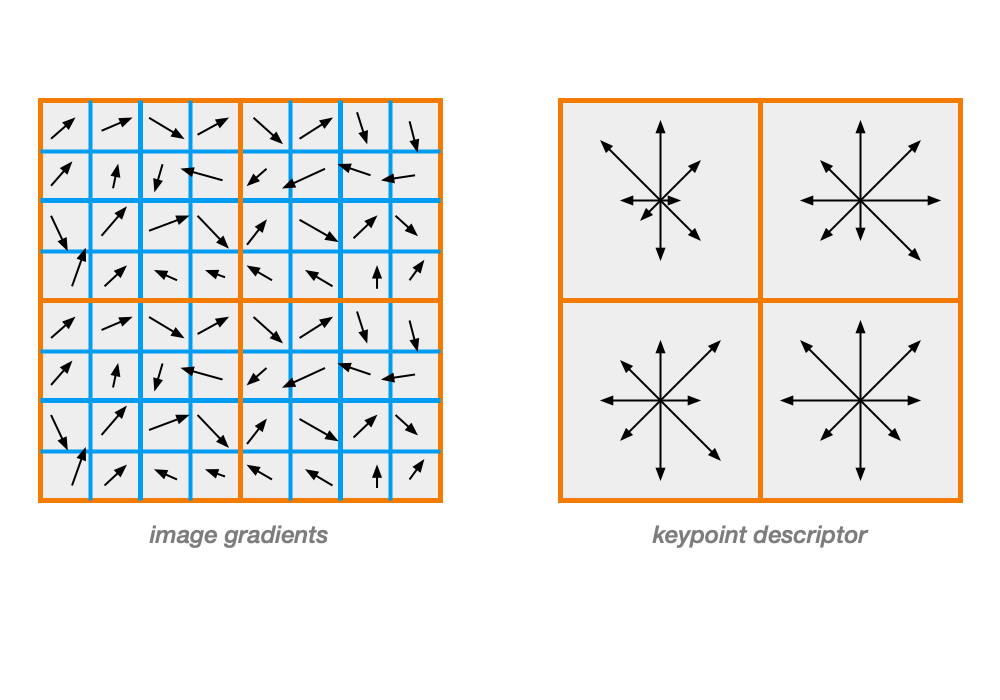
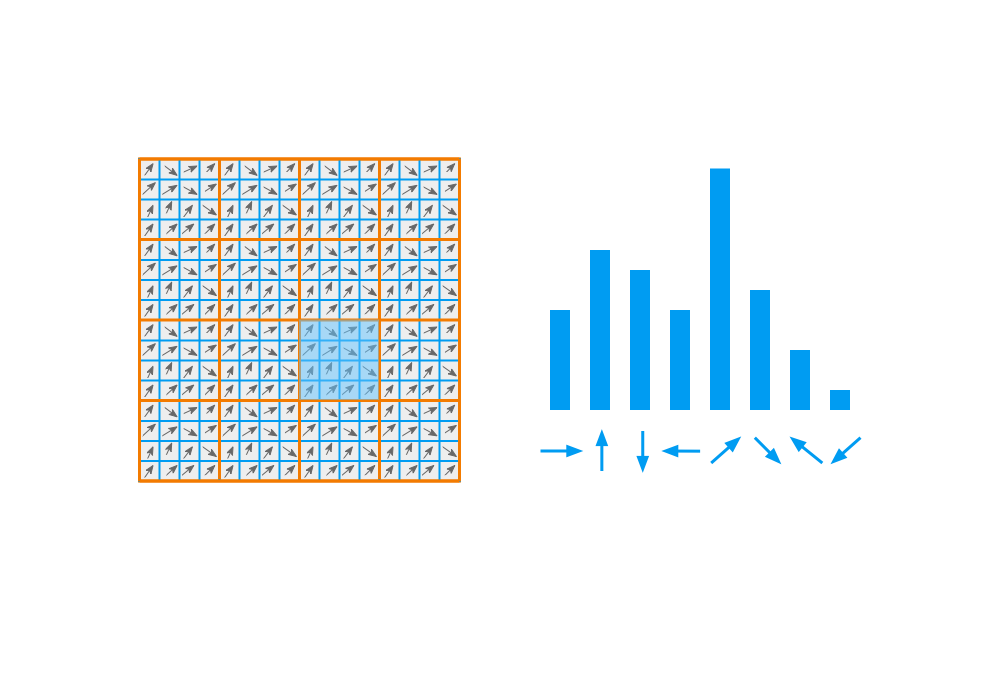
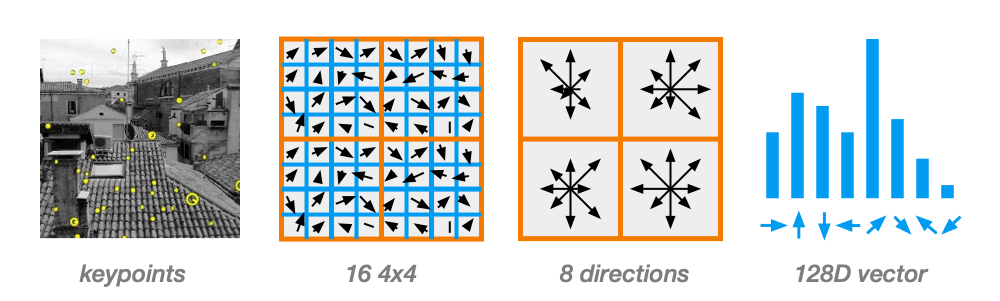
Compute image gradients in local 16x16 area at the selected scale.

• Create an array of orientation histograms
• 8 orientations x 4x4 histogram array = 128 dimensions

SIFT Descriptor

SIFT Descriptor

SIFT Descriptor

SIFT Descriptor

SIFT Descriptor

Concatenate all histograms to form a 128D vector.

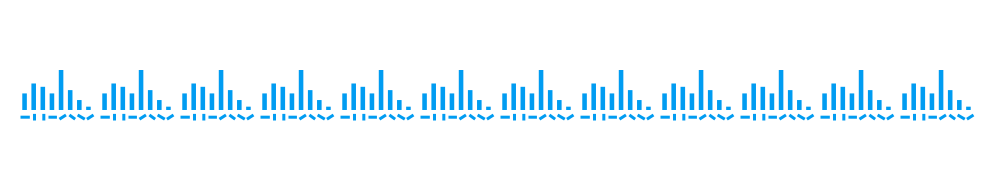
SIFT Descriptor

SIFT Features

Keypoints : Using DoG

Descriptor : Using Gradient Histogram

Dense SIFT

Variation of the SIFT feature, where the keypoints are sampled over a uniform grid in the image domain, rather than using the sparse points from the DoG.

Dense SIFT

At each uniform grid point:

• Compute the SIFT descriptor.
• Cluster the descriptors into a vocabulary.
• K-means clustering.

Distance Matching

Ratio Test

Eliminate ambiguous matches for a query feature \(q\).

1. Find closest descriptors, \(p_1\) and \(p_2\) using Euclidian distance.

2. Test if distance to best match is smaller than a threshold:

\[d(q, p_1) < t\]

3. Accept only if the best match is substantially better than second:

\[\frac{d(q, p_1)}{d(q, p_2)} < \frac{1}{2}\]

Ratio Test

Ratio Test

Lowe’s Ratio test works well.

• There will still be a few outliers.
• Outliers require extra treatment.

Why Binary Descriptors?

Complex features such as SIFT work well, but…

Key Idea of Binary Descriptors

• Select a region around a keypoint.
• Select a set of pixel pairs in that region
• For each pair, compare the intensities.
• concatenate all \(b\) to a string.

\[ b= \begin{cases} 1, & \text{if}\ I(s_1) < I(s_2) \\ 0, & \text{otherwise} \end{cases} \]

Example

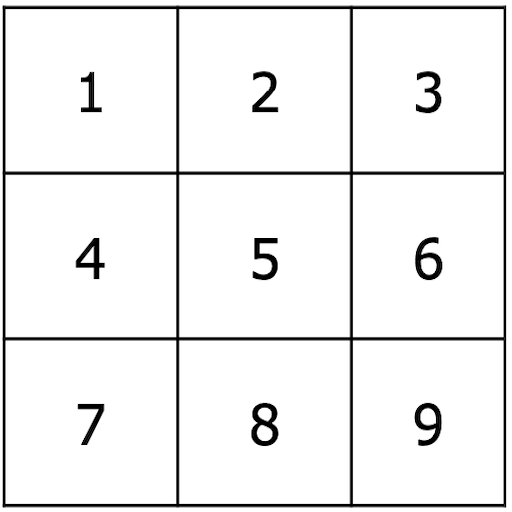
• pairs: \(~\{(5, 1), (5, 9), (4, 6), (8, 2), (3, 7)\}\)
• test: \(~b=0, ~b=0, ~b=0, ~b=1, ~b=1\)
• result: \(~B=00011\)

Advantages of Binary Descriptors

Compact descriptor

• The number of pairs gives the length in bits

Advantages of Binary Descriptors

Fast to compute

• Simply intensity value comparisons

Advantages of Binary Descriptors

Trivial and fast to compare Hamming distance:

\[ d_{Hamming}(B_1, B_2) = sum(xor(B_1, B_2) ) \]

Different binary descriptors differ mainly by the strategy of selecting the pairs.

Important

In order to compare descriptors we must:

• Use the same pairs
• Maintain the same order in which the pairs are tested.

BRIEF

First binary image descriptor.

• Proposed in 2010
• 256 bit descriptor
• Provides five different sampling strategies
• Operations performed on a smoothed image to deal with noise

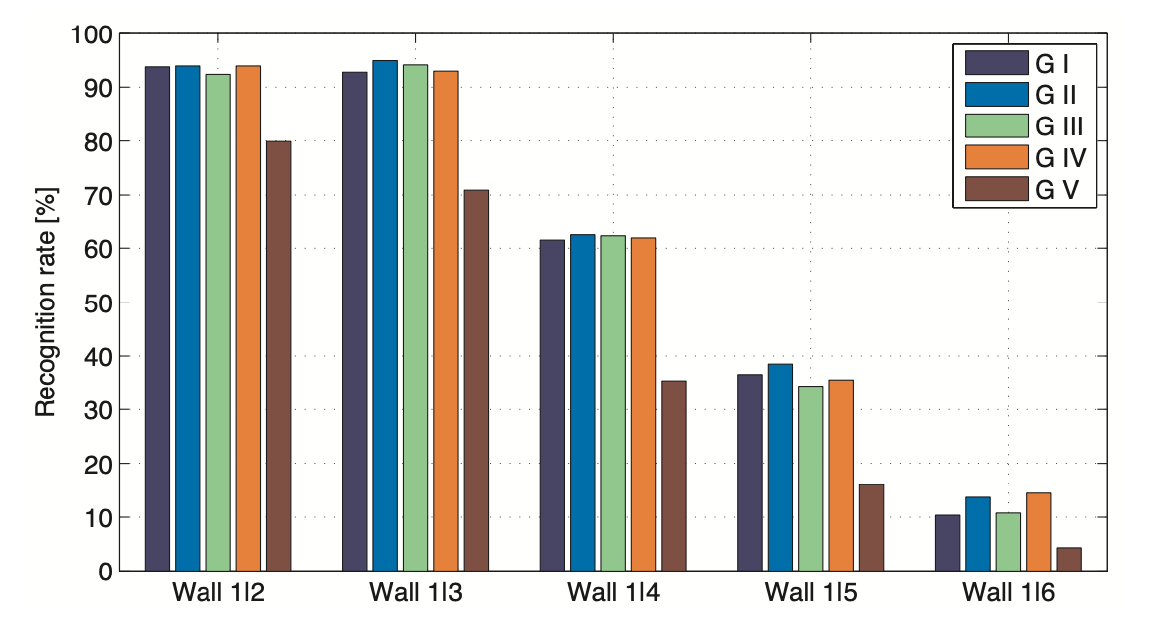
BRIEF sampling pairs

• G I: Uniform random sampling
• G II: Gaussian sampling
• G III: \(~s_1~\) Gaussian; \(~s_2~\) Gaussian centred around \(~s_1~\).
• G IV: Discrete location from a coarse polar grid.
• G V: \(s_1=(0,0)\), \(~s_2~\) are all locations from a coarse polar grid.

ORB

An extension to BRIEF that:

• Adds rotation compensation.
• Learns the optimal sampling pairs.

ORB: Rotation Compensation

Estimates the centre of mass and the main orientation of the local area.

Image moment:

\[ m_{pq} = \sum_{x,y} x^p y^q I(x,y) \]

Centre of Mass, Orientation:

\[ C = \left( \frac{m_{10}}{m_{00}} , \frac{m_{01}}{m_{00}} \right)~, ~\theta = \arctan2(m_{01}, m_{10}) \]

ORB: Rotation Compensation

Rotate the coordinates of all pairs by \(\theta\) around \(C\):

\[ s' = T(C, \theta) s \]

• Use the transformed pixel coordinates for performing the test.
• Rotation is invariant in the image plane.

ORB: Learning Sampling Pairs

Pairs should be uncorrelated.

• each new pair adds new information to the descriptor

Pairs should have high variance.

• makes a feature more discriminative

ORB defines a strategy for selecting 256 pairs, optimising for these properties using a training database.

ORB versus SIFT

• ORB is 100x faster than SIFT
• ORB: 256 bit vs. SIFT: 4096 bit
• ORB is not scale invariant (achievable via an image pyramid)
• ORB mainly in-plane rotation invariant
• ORB has a similar matching performance as SIFT (w/o scale)
• Several modern online systems (e.g. SLAM) use binary features