Visual Features

We can take advantage of these locally distinct features for:

• image classification
• image retrieval
• correspondence between two images
• 3D reconstruction

Visual Features

Keypoint and Descriptor

An important distinction:

Keypoint and Descriptor

keypoint: \((x, ~y)\)

descriptor at the keypoint:

\[ \begin{bmatrix} 0.02 \\ 0.01 \\ 0.10 \\ 0.05 \\ 0.01 \\ ... \end{bmatrix} \]

Keypoints

Finding locally distinct points.

Corners

Corners

Finding Corners

To find corners we need to search for intensity changes in two directions.

Finding Corners

Compute the SSD of pixels in the neighbourhood \(W\) around \((x, ~y)\).

\[ f(x, y) = \sum_{(u, v) \in W_{x,y} } (I(u, v) - I(u + \delta u , v + \delta v))^2 \]

Finding Corners

\[ f(x, y) = \sum_{(u, v) \in W_{x,y} } (I(u, v) - I(u + \delta u , v + \delta v))^2 \]

Using Taylor expansion, with Jacobian \(\left[J_x, J_y \right]\):

\[ I(u + \delta u , v + \delta v) \approx I(u, v) + \left[J_x, J_y \right] \begin{bmatrix} \delta u \\ \delta v \end{bmatrix} \]

Finding Corners

Taylor approximation leads to:

\[ f(x, y) = \sum_{(u, v) \in W_{x,y} } \left( [J_x, J_y] \begin{bmatrix} \delta u \\ \delta v \end{bmatrix}\right)^2 \]

Written in matrix form:

\[ f(x, y) = \sum_{(u, v) \in W_{x,y} } \begin{bmatrix} \delta u \\ \delta v \end{bmatrix}^T \begin{bmatrix} J_x^2 &J_xJ_y \\ J_xJ_y &J_y^2 \end{bmatrix} \begin{bmatrix} \delta u \\ \delta v \end{bmatrix} \]

Finding Corners

Given:

\[ f(x, y) = \sum_{(u, v) \in W_{x,y} } \begin{bmatrix} \delta u \\ \delta v \end{bmatrix}^T \begin{bmatrix} J_x^2 &J_xJ_y \\ J_xJ_y &J_y^2 \end{bmatrix} \begin{bmatrix} \delta u \\ \delta v \end{bmatrix} \]

Move the summation inside the matrix:

\[ f(x, y) = \begin{bmatrix} \delta u \\ \delta v \end{bmatrix}^T \begin{bmatrix} \sum_{W}J_x^2 &\sum_{W}J_xJ_y \\ \sum_{W}J_xJ_y &\sum_{W}J_y^2 \end{bmatrix} \begin{bmatrix} \delta u \\ \delta v \end{bmatrix} \]

Structure Matrix

• The structure matrix is key to finding edges and corners.
• Encodes the image intensity changes in a local area.
• built from image gradients.

\[ M = \begin{bmatrix} \sum_{W}J_x^2 &\sum_{W}J_xJ_y \\ \sum_{W}J_xJ_y &\sum_{W}J_y^2 \end{bmatrix} \]

Structure Matrix

Matrix built from image gradients.

\[ M = \begin{bmatrix} \sum_{W}J_x^2 &\sum_{W}J_xJ_y \\ \sum_{W}J_xJ_y &\sum_{W}J_y^2 \end{bmatrix} \]

Jacobians computed by convolution with gradient kernel, e.g. Sobel:

\[ \begin{aligned} J_x^2 &= (D_x * I)^2 \\ J_xJ_y &= (D_x * I) (D_y * I) \\ J_y^2 &= (D_y * I)^2 \end{aligned} \]

Structure Matrix

Matrix built from image gradients.

\[ M = \begin{bmatrix} \sum_{W}J_x^2 &\sum_{W}J_xJ_y \\ \sum_{W}J_xJ_y &\sum_{W}J_y^2 \end{bmatrix} \]

Jacobians using Sobel:

\[ D_x = \begin{bmatrix} 1 & 2 & 1 \\ 0 & 0 & 0 \\ \llap{-}1 & \llap{-}2 & \llap{-}1 \end{bmatrix}~, ~ D_y = \begin{bmatrix} 1 & 0 & \llap{-}1 \\ 2 & 0 & \llap{-}2 \\ 1 & 0 & \llap{-}1 \end{bmatrix} \]

Structure Matrix

Summarises the dominant gradient directions around a point.

\[ M = \begin{bmatrix} \sum_{W}J_x^2 &\sum_{W}J_xJ_y \\ \sum_{W}J_xJ_y &\sum_{W}J_y^2 \end{bmatrix} \]

Structure Matrix

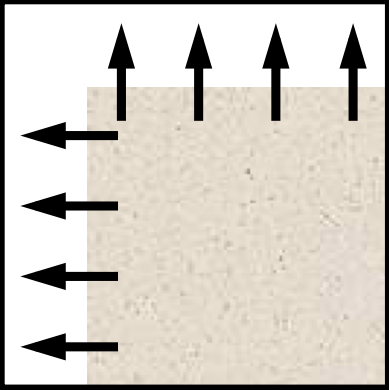
\[ M = \begin{bmatrix} \gg 1 &\approx 0 \\ \approx 0 &\gg 1 \end{bmatrix} \]

Structure Matrix

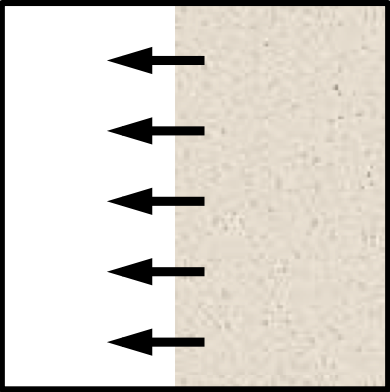
\[ M = \begin{bmatrix} \gg 1 &\approx 0 \\ \approx 0 &\approx 0 \end{bmatrix} \]

Structure Matrix

\[ M = \begin{bmatrix} \approx 0 &\approx 0 \\ \approx 0 &\approx 0 \end{bmatrix} \]

Corners from Structure Matrix

Consider points as corners if their structure matrix has two large Eigenvalues.

\[ M = \begin{bmatrix} \gg 1 &\approx 0 \\ \approx 0 &\gg 1 \end{bmatrix} \]

Harris, Shi-Tomasi and Förstner

Three similar approaches:

• 1987 Förstner
• 1988 Harris
• 1994 Shi-Tomasi

All rely on the structure matrix.

• Use different criteria for deciding if a point is a corner
• Förstner offers subpixel estimation

Harris Corner Criterion

Criterion:

\[ \begin{aligned} R &= det(M) - k(trace(M))^2 \\ &= \lambda_1 \lambda_2 - k(\lambda_1 + \lambda_2)^2 \end{aligned} \]

with \(k \in [0.04, 0.06]\):

\[ \begin{aligned} |R| &\approx 0 \Rightarrow \lambda_1 \approx \lambda_2 \approx 0 \\ R &< 0 \Rightarrow \lambda_1 \gg \lambda_2~ or ~\lambda_2 \gg \lambda_1 \\ R &\gg 0 \Rightarrow \lambda_1 \approx \lambda_2 \gg 0 \end{aligned} \]

Shi-Tomasi Criterion

Threshold smallest Eigenvalue:

\[ \lambda_{min}(M) = \frac{trace(M)}{2} - \frac{1}{2} \sqrt{trace(M)^2 - 4 det(M)} \]

corner:

\[ \lambda_{min}(M) \geq T \]

Förstner Criterion

• Similar to Harris corner detector.
• Criterion defined on the covariance matrix of possible shifts - inverse of \(M\).
• Similar criteria on error ellipse.

Non-Maxima Suppression

Within a local region, look for position with maximum value \(R\).

Which would be maximum here?

Harris Corner Example

Corner Detection in Practice

• RGB to grey scale conversion.
• Real images are noisy, so smoothing is recommended.

Corner Detection Algorithm

Corner Detectors Compared

• All three detectors perform similarly.
• Förstner was first and also described subpixel estimation.
• Harris became the most popular corner detector.
• Shi-Tomasi seems to slightly outperform Harris.
• Many libraries use Shi-Tomasi as the default corner detector.

DoG Keypoints

A variant of corner detection.

• Provides responses at corners, edges, and blobs.
• Blob = mainly constant region but different to its surroundings.

DoG over Scale Space Pyramid

Over different image pyramid levels

Difference of Gaussians

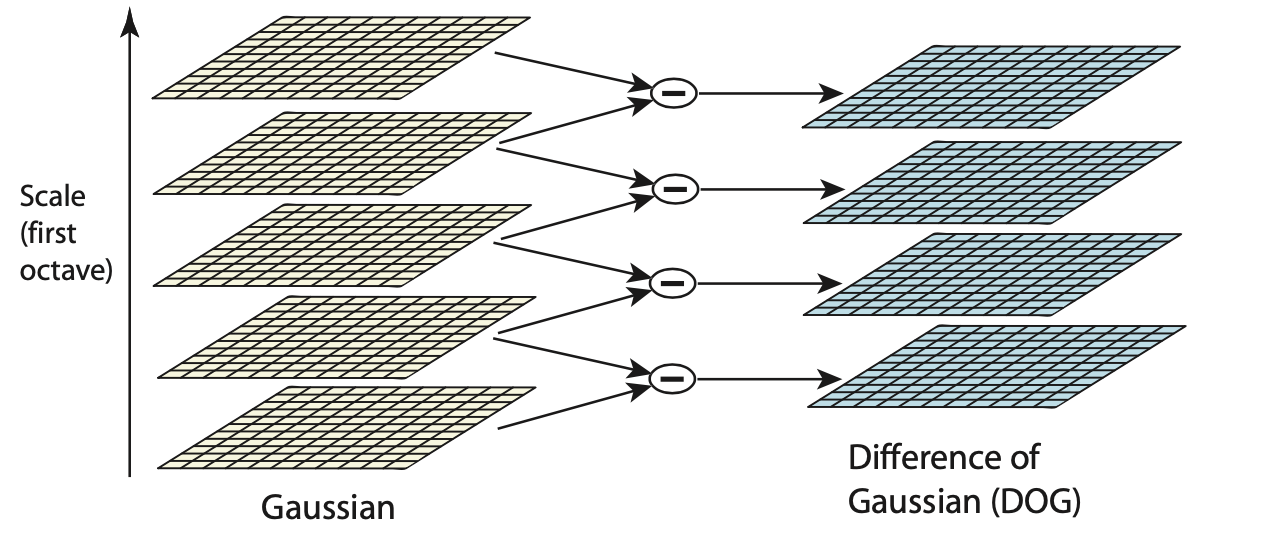
Difference of Gaussians

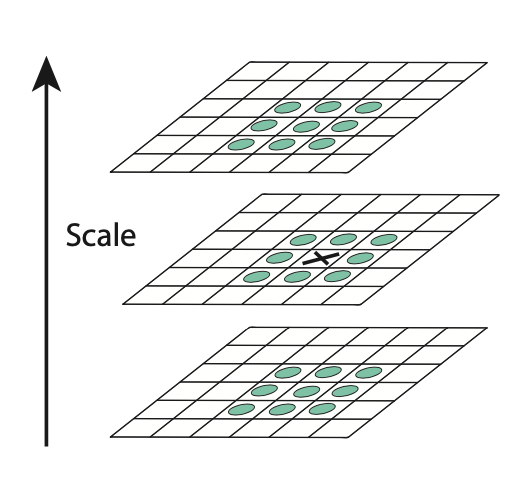
We search in \((x, y)\) and in the third dimension.

Difference of Gaussians

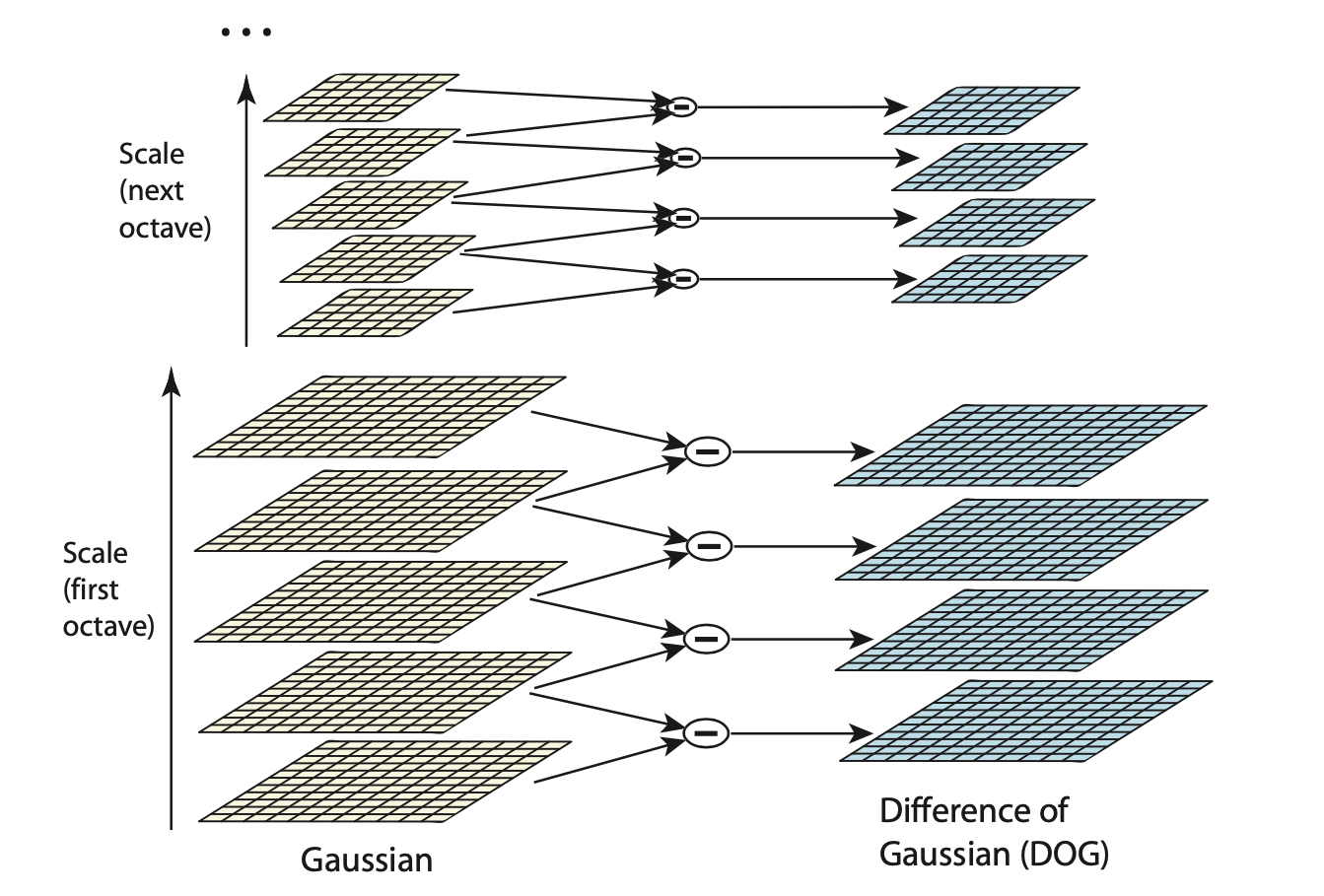
Difference of Gaussians

Difference of Gaussians

Difference of Gaussians

Blurring filters out high-frequencies (noise).

Subtracting differently blurred images from each other only keeps the frequencies that lie between the blur level of both images

DoG acts as a band-pass filter.

Difference of Gaussians

keypoints are the local extrema in the DoG over different scales.

Difference of Gaussians

The DoG finds blob-like and corner-like image structures but also has strong responses along edges.